TDLR; A Python implementation of grouped radial convergence plots based on code from the Rhodium library. This script is will be added to Antonia’s repository for Radial Convergence Plots.
Radial convergence plots are a useful tool for visualizing results of Sobol Sensitivities analyses. These plots array the model parameters in a circle and plot the first order, total order and second order Sobol sensitivity indices for each parameter. The first order sensitivity is shown as the size of a closed circle, the total order as the size of a larger open circle and the second order as the thickness of a line connecting two parameters.
In May, Antonia created a new Python library to generate Radial Convergence plots in Python, her post can be found here and the Github repository here. I’ve been working with the Rhodium Library a lot recently and found that it contained a Radial Convergence Plotting function with the ability to plot grouped output, a functionality that is not present in Antonia’s repository. This function produces the same plots as Calvin’s R package. Adding a grouping functionality allows the user to color code the visualization to improve the interpretability of the results. In the code below I’ve adapted the Rhodium function to be a standalone Python code that can create visualizations from raw output of the SALib library. When used on a policy for the Lake Problem, the code generates the following plot shown in Figure 1.
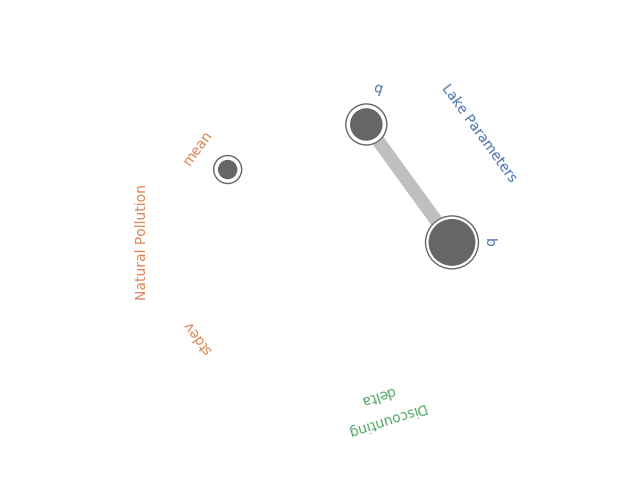
Figure 1: Example Radial Convergence Plot for the Lake Problem reliability objective. Each of the points on the plot represents a sampled uncertain parameter in the model. The size of the filled circle represents the first order Sobol Sensitivity Index, the size of the open circle represents the total order Sobol Sensitivty Index and the thickness of lines between points represents the second order Sobol Sensitivity Index.
import numpy as np
import itertools
import matplotlib.pyplot as plt
import seaborn as sns
import math
sns.set_style('whitegrid', {'axes_linewidth': 0, 'axes.edgecolor': 'white'})
def is_significant(value, confidence_interval, threshold="conf"):
if threshold == "conf":
return value - abs(confidence_interval) > 0
else:
return value - abs(float(threshold)) > 0
def grouped_radial(SAresults, parameters, radSc=2.0, scaling=1, widthSc=0.5, STthick=1, varNameMult=1.3, colors=None, groups=None, gpNameMult=1.5, threshold="conf"):
# Derived from https://github.com/calvinwhealton/SensitivityAnalysisPlots
fig, ax = plt.subplots(1, 1)
color_map = {}
# initialize parameters and colors
if groups is None:
if colors is None:
colors = ["k"]
for i, parameter in enumerate(parameters):
color_map[parameter] = colors[i % len(colors)]
else:
if colors is None:
colors = sns.color_palette("deep", max(3, len(groups)))
for i, key in enumerate(groups.keys()):
#parameters.extend(groups[key])
for parameter in groups[key]:
color_map[parameter] = colors[i % len(colors)]
n = len(parameters)
angles = radSc*math.pi*np.arange(0, n)/n
x = radSc*np.cos(angles)
y = radSc*np.sin(angles)
# plot second-order indices
for i, j in itertools.combinations(range(n), 2):
#key1 = parameters[i]
#key2 = parameters[j]
if is_significant(SAresults["S2"][i][j], SAresults["S2_conf"][i][j], threshold):
angle = math.atan((y[j]-y[i])/(x[j]-x[i]))
if y[j]-y[i] < 0:
angle += math.pi
line_hw = scaling*(max(0, SAresults["S2"][i][j])**widthSc)/2
coords = np.empty((4, 2))
coords[0, 0] = x[i] - line_hw*math.sin(angle)
coords[1, 0] = x[i] + line_hw*math.sin(angle)
coords[2, 0] = x[j] + line_hw*math.sin(angle)
coords[3, 0] = x[j] - line_hw*math.sin(angle)
coords[0, 1] = y[i] + line_hw*math.cos(angle)
coords[1, 1] = y[i] - line_hw*math.cos(angle)
coords[2, 1] = y[j] - line_hw*math.cos(angle)
coords[3, 1] = y[j] + line_hw*math.cos(angle)
ax.add_artist(plt.Polygon(coords, color="0.75"))
# plot total order indices
for i, key in enumerate(parameters):
if is_significant(SAresults["ST"][i], SAresults["ST_conf"][i], threshold):
ax.add_artist(plt.Circle((x[i], y[i]), scaling*(SAresults["ST"][i]**widthSc)/2, color='w'))
ax.add_artist(plt.Circle((x[i], y[i]), scaling*(SAresults["ST"][i]**widthSc)/2, lw=STthick, color='0.4', fill=False))
# plot first-order indices
for i, key in enumerate(parameters):
if is_significant(SAresults["S1"][i], SAresults["S1_conf"][i], threshold):
ax.add_artist(plt.Circle((x[i], y[i]), scaling*(SAresults["S1"][i]**widthSc)/2, color='0.4'))
# add labels
for i, key in enumerate(parameters):
ax.text(varNameMult*x[i], varNameMult*y[i], key, ha='center', va='center',
rotation=angles[i]*360/(2*math.pi) - 90,
color=color_map[key])
if groups is not None:
for i, group in enumerate(groups.keys()):
print(group)
group_angle = np.mean([angles[j] for j in range(n) if parameters[j] in groups[group]])
ax.text(gpNameMult*radSc*math.cos(group_angle), gpNameMult*radSc*math.sin(group_angle), group, ha='center', va='center',
rotation=group_angle*360/(2*math.pi) - 90,
color=colors[i % len(colors)])
ax.set_facecolor('white')
ax.set_xticks([])
ax.set_yticks([])
plt.axis('equal')
plt.axis([-2*radSc, 2*radSc, -2*radSc, 2*radSc])
#plt.show()
return fig
The code below implements this function using the SALib to conduct a Sobol Sensitivity Analysis on the Lake Problem to produce Figure 1.
import numpy as np
import itertools
import matplotlib.pyplot as plt
import math
from SALib.sample import saltelli
from SALib.analyze import sobol
from lake_problem import lake_problem
from grouped_radial import grouped_radial
# Define the problem for SALib
problem = {
'num_vars': 5,
'names': ['b', 'q', 'mean', 'stdev', 'delta'],
'bounds': [[0.1, 0.45],
[2.0, 4.5],
[0.01, 0.05],
[0.001, 0.005],
[0.93, 0.99]]
}
# generate Sobol samples
param_samples = saltelli.sample(problem, 1000)
# extract each parameter for input into the lake problem
b_samples = param_samples[:,0]
q_samples = param_samples[:,1]
mean_samples = param_samples[:,2]
stdev_samples = param_samples[:,3]
delta_samples = param_samples[:,4]
# run samples through the lake problem using a constant policy of .02 emissions
pollution_limit = np.ones(100)*0.02
# initialize arrays to store responses
max_P = np.zeros(len(param_samples))
utility = np.zeros(len(param_samples))
inertia = np.zeros(len(param_samples))
reliability = np.zeros(len(param_samples))
# run model across Sobol samples
for i in range(0, len(param_samples)):
print("Running sample " + str(i) + ' of ' + str(len(param_samples)))
max_P[i], utility[i], inertia[i], reliability[i] = lake_problem(pollution_limit,
b=b_samples[i],
q=q_samples[i],
mean=mean_samples[i],
stdev=stdev_samples[i],
delta=delta_samples[i])
#Get sobol indicies for each response
SA_max_P = sobol.analyze(problem, max_P, print_to_console=False)
SA_reliability = sobol.analyze(problem, reliability, print_to_console=True)
SA_inertia = sobol.analyze(problem, inertia, print_to_console=False)
SA_utility = sobol.analyze(problem, utility, print_to_console=False)
# define groups for parameter uncertainties
groups={"Lake Parameters" : ["b", "q"],
"Natural Pollution" : ["mean", "stdev"],
"Discounting" : ["delta"]}
fig = grouped_radial(SA_reliability, ['b', 'q', 'mean', 'stdev', 'delta'], groups=groups, threshold=0.025)
plt.show()