Search with Multiobjective Evolutionary Algorithms (MOEAs) is inherently stochastic. MOEAs are initialized with a random population of solutions that serve as the starting point for the multiobjective search, if the algorithm gets “lucky”, the initial population may contain points in an advantageous region of the decision space that give the algorithm a head start on the search. On the other hand, the initial population may only contain solutions in difficult regions of the decision space, which may slow the discovery of quality solutions. To overcome the effects of initial parameterization, we perform a random seed analysis which involves running an ensemble of searches, each starting with a randomly sampled set of initial conditions which we’ll here on refer to as a “random seed”. We combine search results across all random seeds to generate a “reference set” which contains only the best (Pareto non-dominated) solutions across the ensemble.
Tracking the algorithm’s performance during search is an important part of a random seed analysis. When we use MOEAs to solve real world problems (ie. problems that don’t have analytical solutions), we don’t know the true Pareto set a priori. To determine if an algorithm has discovered an acceptable approximation of the true Pareto set, we must measure it’s performance across the search, and only end our analysis if we can demonstrate the search has ceased improving (of course this is not criteria for true convergence as it is possible the algorithm has simply failed to find better solutions to the problem, this is why performing rigorous diagnostic studies such as Zatarain et al., 2016 is important for understanding how various MOEAs perform in real world problems). To measure MOEA search performance, we’ll use hypervolume , a metric that captures both convergence and diversity of a given approximation set (Knowles and Corne, 2002; Zitzler et al., 2003). Hypervolume represents the fraction of the objective space that is dominated by an approximation set, as shown in Figure 1 (from Zatarain et al., 2017). For more information on MOEA performance metrics, see Joe’s post from 2013.

Figure 1: A 2 objective example of hypervolume from Zatarain et al,. 2017. To calculate hypervolume, an offset, delta, is taken from the bounds of the approximation set to construct a “reference point”. The hypervolume is a measure of the volume of the objective space between the approximation set and the reference point. A larger hypervolume indicates a better approximation set.
This post will demonstrate how to perform a random seed analysis and runtime diagnostics using the Matlab wrapper for the serial Borg MOEA (for background on the Borg MOEA, see Hadka and Reed, 2013). I’ll use the DTLZ2 3 objective test problem as an example, which tasks the algorithm with approximating a spherical Pareto-optimal front (Deb et al,. 2002). I’ve created a Github repository with relevant code, you can find it here.
In this demonstration, I’ll use the Matlab IDE and Bash shell scripts called from a Linux terminal (Window’s machines can use Cygwin, a free Linux emulator). If you are unfamiliar with using a Linux terminal, you can find a tutorial here. To perform runtime diagnostics, I’ll use the MOEAFramework, a Java library that you can download here (the demo version will work just fine for our purposes).
A modified Matlab wrapper that produces runtime files
In order to track search performance across time, we need snapshots of Borg’s archive during the search. In the parallel “master-worker” and “multi-master” versions of Borg, these snapshots are generated by the Borg C library in the form of “runtime” files. The snapshots provided by the runtime files contain information on the number of function evaluations completed (NFE), elapsed time, operator probabilities, number of improvements, number of restarts, population size, archive size and the decision variables and objectives within the archive itself.
To my knowledge, the current release of the serial Borg Matlab wrapper does not print runtime files. To perform runtime diagnostics, I had to modify the wrapper file, nativeborg.cpp. I’ve posted my edited version to the aforementioned Github repository.
Performing random seed analysis and runtime diagnostics
To perform a random seed analysis and runtime diagnostics with the Matlab wrapper, follow these steps:
1) Download the Borg MOEA and compile the Matlab wrapper
To request access to the Borg MOEA, complete step 2 of Jazmin’s introduction to Borg, found here . To run Borg with Matlab you must compile a MEX file, instructions for compiling for Windows can be found here, and here for Linux/Mac.
Once you’ve downloaded and compiled Borg for Matlab, clone the Github repository I’ve created and replace the nativeborg.cpp file from the Borg download with the edited version from the repository. Next, create three new folders in your working directory, one called “Runtime” and another called “Objectives” and the third called “metrics”. Make sure your working directory contains the following files:
- borg.c
- borg.h
- mt19937ar.c
- mt19937ar.h
- nativeborg.cpp (version from the Git repository)
- borg.m
- DTLZ2.m (test problem code, supplied from Github repository)
- calc_runtime_metrics.sh
- append_hash.sh
- MOEAFramework-2.12-Demo.jar
2) Use Matlab to run the Borg MOEA across an ensemble of random seeds
For this example we’ll use 10 seeds with 30,000 NFE each. We’ll print runtime snapshots every 500 NFE.
To run DTLZ2 across 10 seeds, run the following script in Matlab:
for i = [1:10]
[vars, objs, runtime] = borg(12,3,0, @DTLZ2, 30000, zeros(1,12),ones(1,12), [0.01, 0.01, 0.01], {'frequency',500, 'seed', i});
objFile = sprintf('Objectives/DTLZ2_3_S%i.obj',i);
dlmwrite(objFile, objs, 'Delimiter', ' ');
end
The for loop above iterates across 10 random initialization of the algorithm. The first line within the for loop calls the Borg MOEA and returns decision variables (vars), objective values (objs) and a struct with basic runtime information. This function will also produce a runtime file, which will be printed in the Runtime folder created earlier (more on this later).
The second line within the for loop creates a string containing the name of a file to store the seed’s objectives and the third line prints the final objectives to this file.
3) Calculate the reference set across random seeds using the MOEAFramework
The 10 .obj files created in step two containing the final archives from each random seed. For our analysis, we want to generate a “reference set” of the best solutions across all seeds. To generate this set, we’ll use built in tools from the MOEAFramework. The MOEAFramework requires that all .obj files have “#” at the end of the file, which is annoying to add in Matlab. To get around this, I’ve written a simple Bash script called “append_hash.sh”.
In your Linux terminal navigate to the working directory with your files (the folder just above Objectives) and run the Bash script like this:
./append_hash.sh
Now that the hash tags have been appended to each .obj files, create an overall reference set by running the following command in your Linux Terminal.
java -cp MOEAFramework-2.12-Demo.jar org.moeaframework.analysis.sensitivity.ResultFileSeedMerger -d 3 -e 0.01,0.01,0.01 -o Borg_DTLZ2_3.reference Objectives/*.obj
This command calls the MOEAFramework’s ResultFileMerger tool, which will merge results across random seeds. The -d flag specifies the number of objectives in our problem (3), the -e flag specifies the epsilons for each objective (.01 for all 3 objectives), the -o flag specifies the name of our newly created reference set file and the Objectives/*.obj tells the MOEAFramework to merge all files in the Objectives folder that have the extension “.obj”. This command will generate a new file named “Borg_DTLZ2_3.reference”, which will contain 3 columns, each corresponding to one objective. If we load this file into matlab and plot, we get the following plot of our Pareto approximate set.
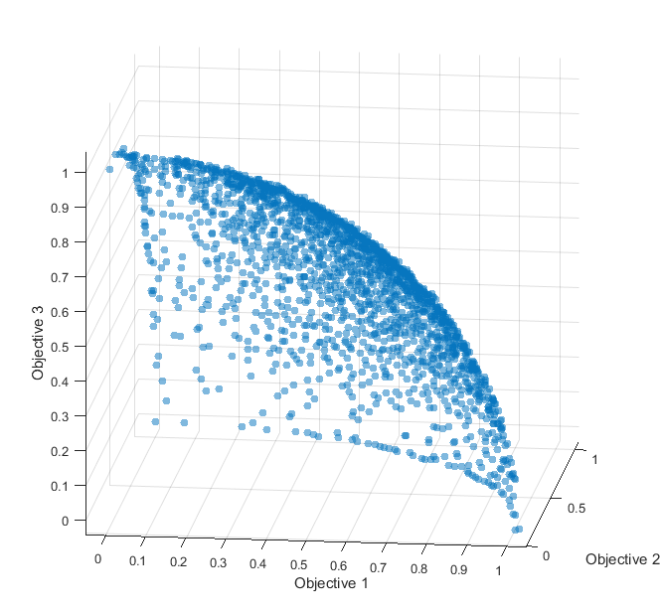
Figure 2: The reference set generated by the Borg Matlab wrapper using 30,000 NFE.
4) Calculate and visualize runtime hypervolumes
We now have a reference set representing the best solutions across our random seeds. A final step in our analysis is to examine runtime data to understand how the search progressed across function evaluations. We’ll again use the MOEAFramework to examine each seed’s hypervolume at the distinct runtime snapshots provided in the .runtime files. I’ve written a Bash script to call the MOEAFramework, which is provided in the Git repository as “calc_runtime_metrics.sh” and reproduced below:
#/bin/bash
NSEEDS=10
SEEDS=$(seq 1 ${NSEEDS})
JAVA_ARGS="-cp MOEAFramework-2.12-Demo.jar"
for SEED in ${SEEDS}
do
java ${JAVA_ARGS} org.moeaframework.analysis.sensitivity.ResultFileEvaluator -d 3 -i ./Runtime/runtime_S${SEED}.runtime -r Borg_DTLZ2_3.reference -o ./metrics/Borg_DTLZ2_3_S${SEED}.metrics
done
To execute the script in your terminal enter:
./calc_runtime_metrics.sh
The above command will generate 10 .metrics files inside the metrics folder, each .metric file contains MOEA performance metrics for one randome seed, hypervolume is in the first column, each row represents a different runtime snapshot. It’s important to note that the hypervolume calculated by the MOEAFramework here is the absolute hypervolume, but what we really want in this situation is the relative hypervolume to the reference set (ie the hypervolume achieved at each runtime snapshot divided by the hypervolume of the reference set). To calculate the hypervolume of the reference set, follow the steps presented in step 2 of Jazmin’s blog post (linked here), and divide all runtime hypervolumes by this value.
To examine runtime peformance across random seeds, we can load each .metric file into Matlab and plot hypervolume against NFE. The runtime hypervolume for the DTLZ2 3 objective test case I ran is shown in Figure 3 below.

Figure 3: Runtime results for the DTLZ2 3 objective test case
Figure 3 shows that while there is some variance across the seeds, they all approach the hypervolume of the reference set after about 10,000 NFE. This leveling off of our search across many initial parameterizations indicates that our algorithm has likely converged to a final approximation of our Pareto set. If this plot had yielded hypervolumes that were still increasing after the 30,000 NFE, it would indicate that we need to extend our search to a higher number of NFE.
References
Deb, K., Thiele, L., Laumanns, M. Zitzler, E., 2002. Scalable multi-objective optimization test problems, Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02, (1), 825-830
Hadka, D., Reed, P., 2013. Borg: an auto-adaptive many-objective evolutionary computing
framework. Evol. Comput. 21 (2), 231–259.
Knowles, J., Corne, D., 2002. On metrics for comparing nondominated sets. Evolutionary
Computation, 2002. CEC’02. Proceedings of the 2002 Congress on. 1. IEEE, pp. 711–716.
Zatarain Salazar, J., Reed, P.M., Herman, J.D., Giuliani, M., Castelletti, A., 2016. A diagnostic assessment of evolutionary algorithms for multi-objective surface water
reservoir control. Adv. Water Resour. 92, 172–185.
Zatarain Salazar, J. J., Reed, P.M., Quinn, J.D., Giuliani, M., Castelletti, A., 2017. Balancing exploration, uncertainty and computational demands in many objective reservoir optimization. Adv. Water Resour. 109, 196-210
Zitzler, E., Thiele, L., Laumanns, M., Fonseca, C.M., Da Fonseca, V.G., 2003. Performance
assessment of multiobjective optimizers: an analysis and review. IEEE Trans. Evol.
Comput. 7 (2), 117–132.

Pingback: Performing Experiments on HPC Systems – Water Programming: A Collaborative Research Blog
Pingback: Visualizing the diversity of a Pareto front approximation using RadVis – Water Programming: A Collaborative Research Blog
Pingback: Visualizing the diversity of a Pareto front approximation using RadVis – Hydrogen Water
Dear Sir
I am not able to generate runtime file within the Runtime folder after following all the steps
Regards